What is a Binary Search Tree

A Binary Search Tree (BST) is a binary tree where each node has a key and meet the following requirements:

• The left subtree of a node contains nodes with keys smaller than the node's key
• The right subtree of a node contains nodes with keys larger than the node's key
• The left and right subtree are binary search trees

 

Here is how a node could look like. For simplicity, the key has type Key and the value has type Value.

   public class Node
   {
       public Key Key;

       // associated value
       public Value Value;
       public Node Left;
       public Node Right;

       public Node(Key key, Value value)
       {
           Key = key;
           Value = value;
       }
   }

Examples

Best case

 

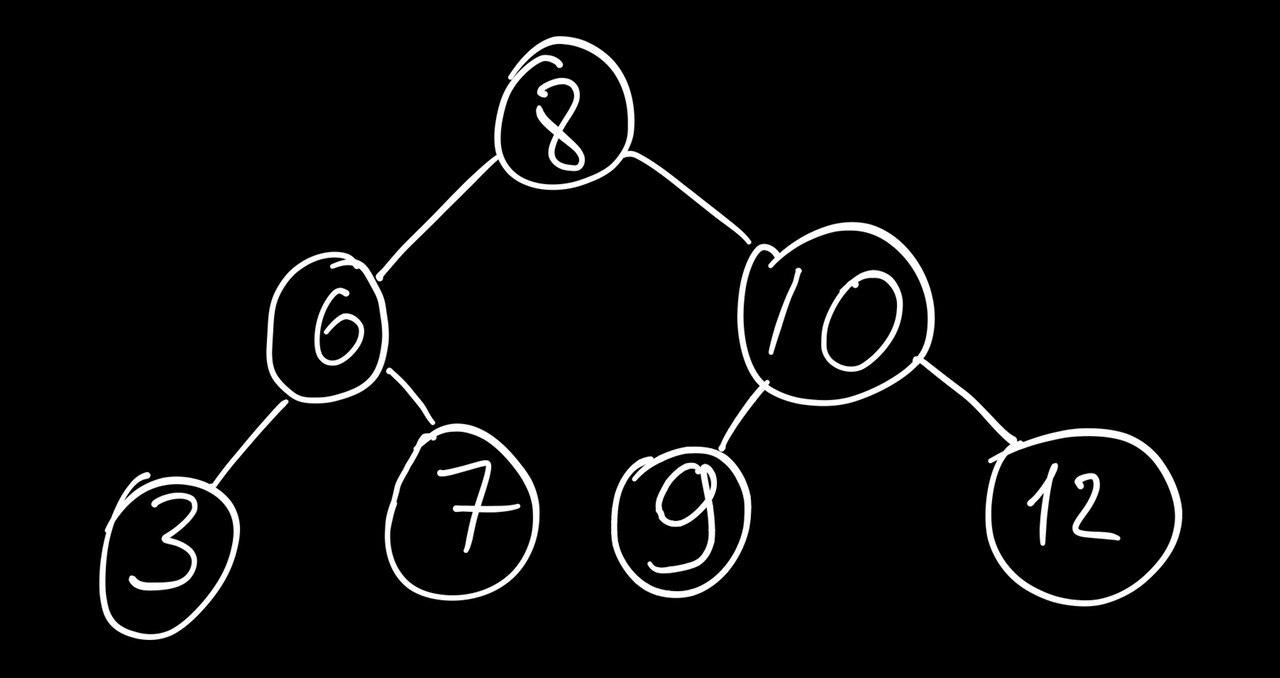
Typical case

 

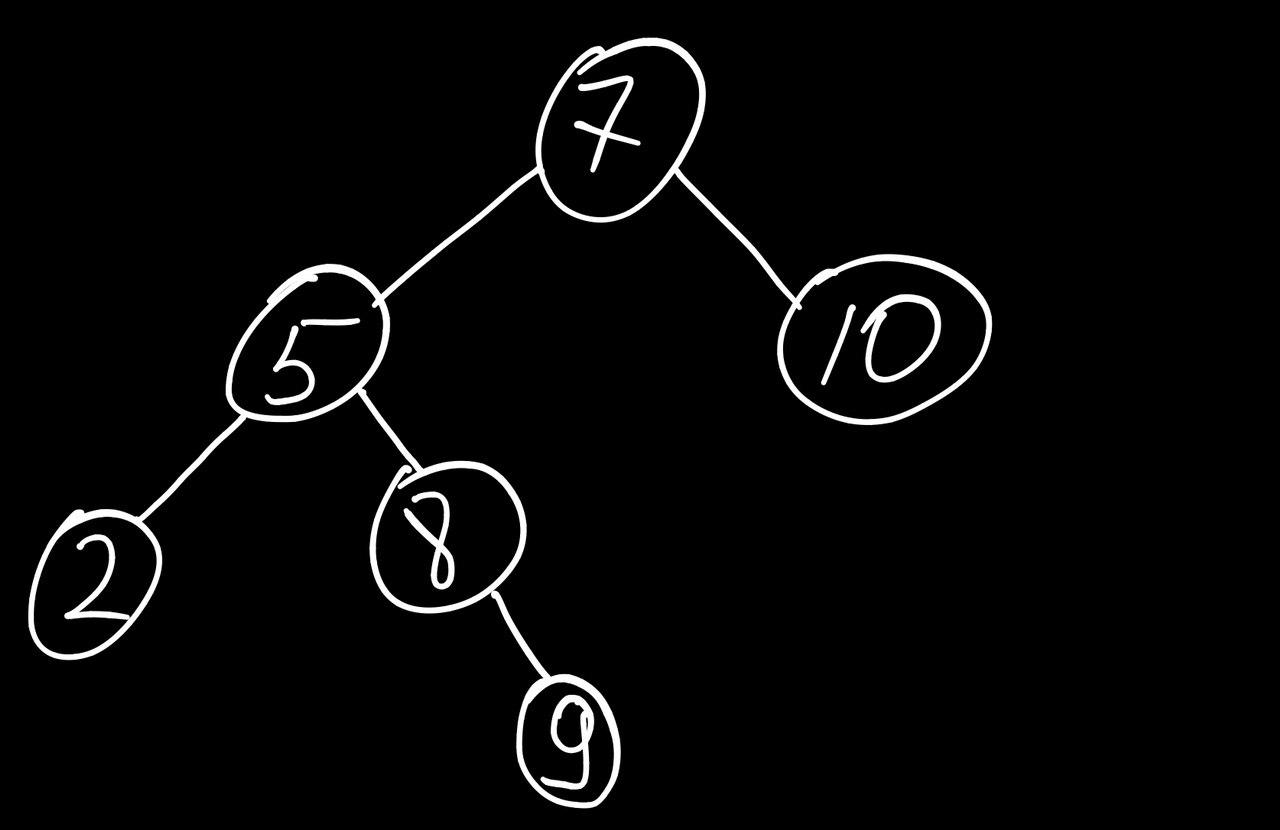
Worst case

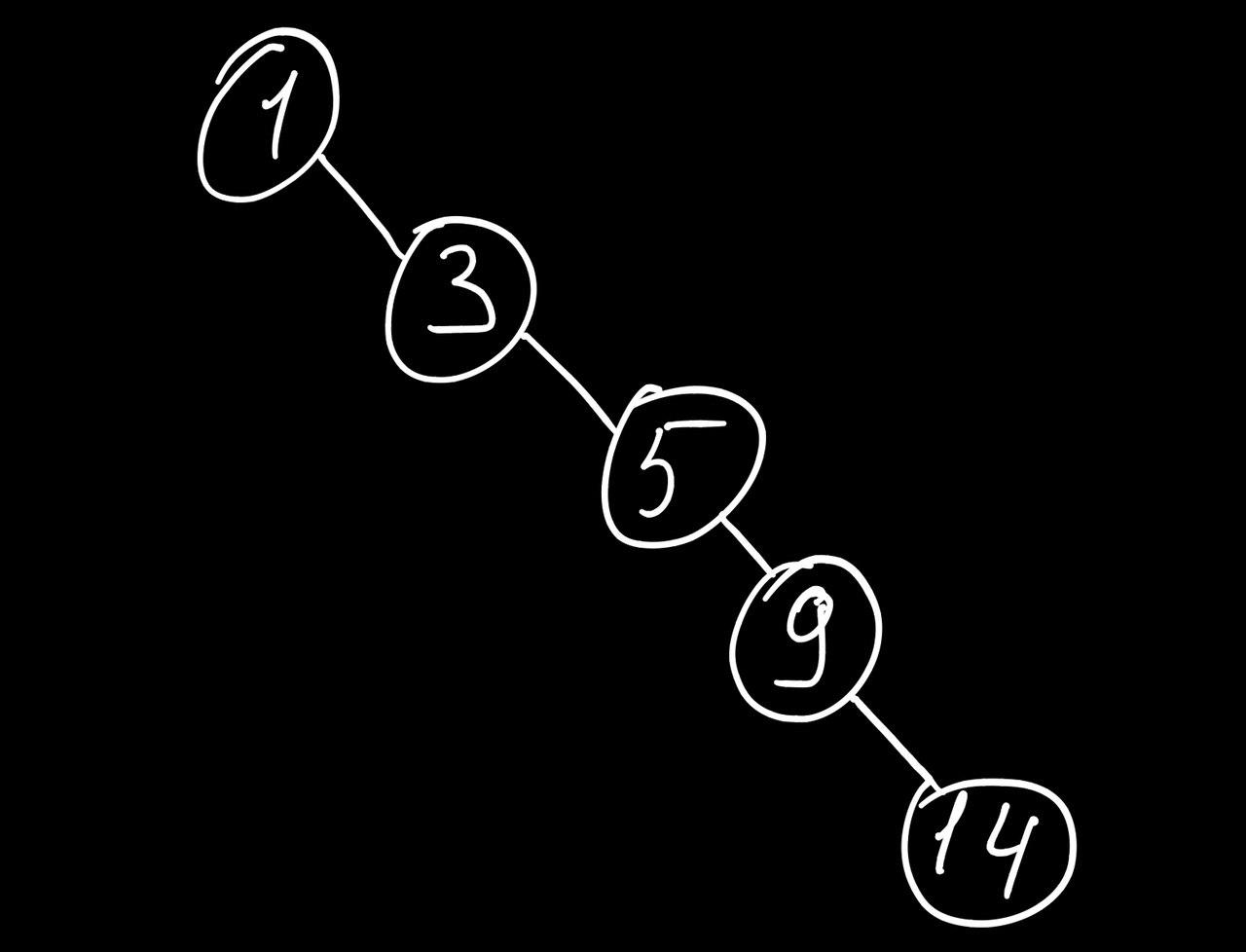
Tree operations

Search operation

It searches for a node using it’s key, and returns it’s value.

the search operation starts from the root node

• if it’s less than, then go left
• if it’s greater than, go right
• if it’s equal, we are done, return a value
• If the tree is empty, or we reached null link, return null. We have a search miss.

    public Value Search(string key)
    {
        Node node = root;
        while (node != null)
        {
            int compareResult = key.CompareTo(node.Key);
            if (compareResult < 0)
            {
                node = node.Left;
            }
            else if (compareResult > 0)
            {
                node = node.Right;
            }
            else
            {
                return node.Value;
            }
        }

        return null;
    }

Time complexity: In average cases the time complexity is O(logn), in the worst case O(n)

Put operation

Insert a node of a key and a value in the BST. The method searches the tree recursively until it finds a null link, and all that we need to do is replace that link with a new node. If the key already exists, it updates the value.

    public void Put(Key key, Value value)
    {
        root = Put(root, key, value);
    }

    private Node Put(Node node, Key key, Value value)
    {
        if (node == null)
        {
            return new Node(key, value);
        }
        int compareResult = key.CompareTo(node.Key);
        if (compareResult < 0)
        {
            node.Left = Put(node.Left, key, value);
        }
        else if(compareResult > 0)
        {
            node.Right = Put(node.Right, key, value);
        }
        else if (compareResult == 0)
        {
            node.Value = value;
        }

        return node;
    }

Time complexity: In average cases the time complexity is O(logn), in the worst case O(n)