Binary tree maximum path sum

Given a non empty binary tree, find out the path with a maximum sum.

For this problem, a path is defined as a sequence of nodes where:

• The starting and ending node could be any node in the binary tree
• The path must contain at least one node
• The path does not need to go through the root

Example 1

Input:       -8    
             / \
            2   3
           /   / \
         -4   5   1
             / 
            2 

Output: 11

Explanation: 3 + 5 + 2 + 1

Example 2

Input:     2   
          / \  
         5   3 

Output:  10

Explanation: 2 + 5 + 3

/* Definition for TreeNode
public class TreeNode
{
    public int Value;
    public TreeNode Left;
    public TreeNode Right;

    public TreeNode(int value)
    {
        Value = value;
    }
}
*/
public class Solution
{
    public int MaxPathSum(TreeNode root)
    {
    }
}

Let's see several examples first:

 

 

 

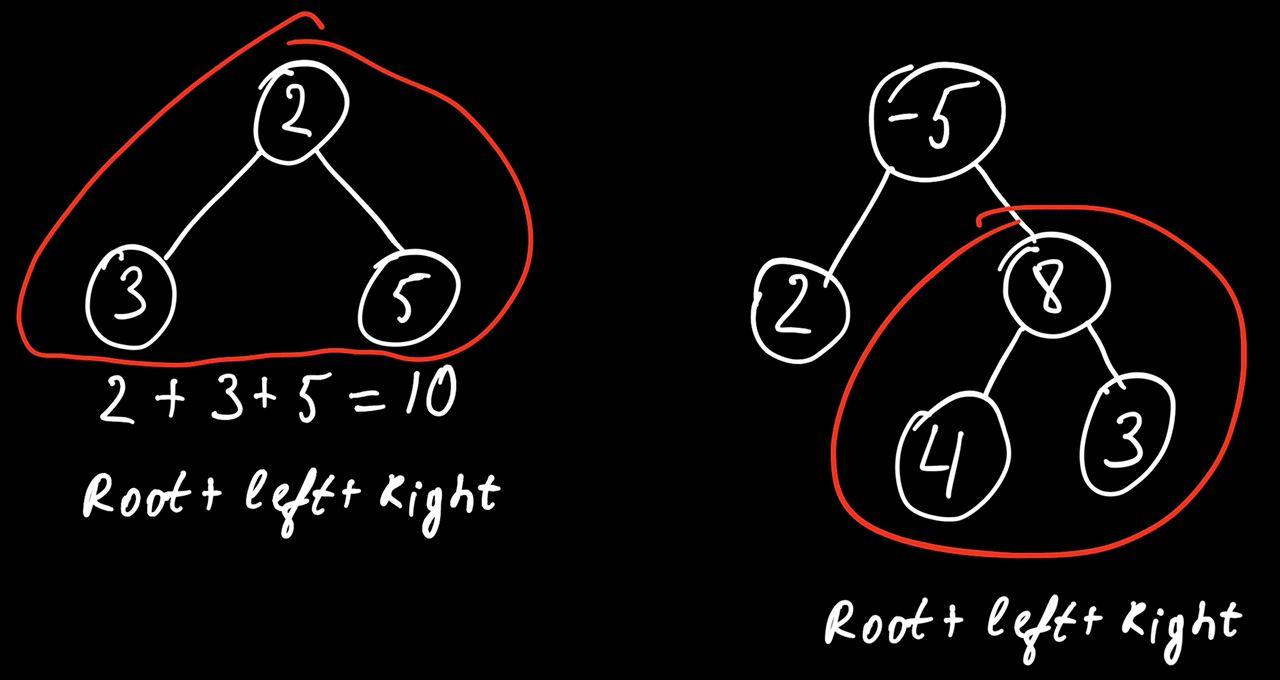
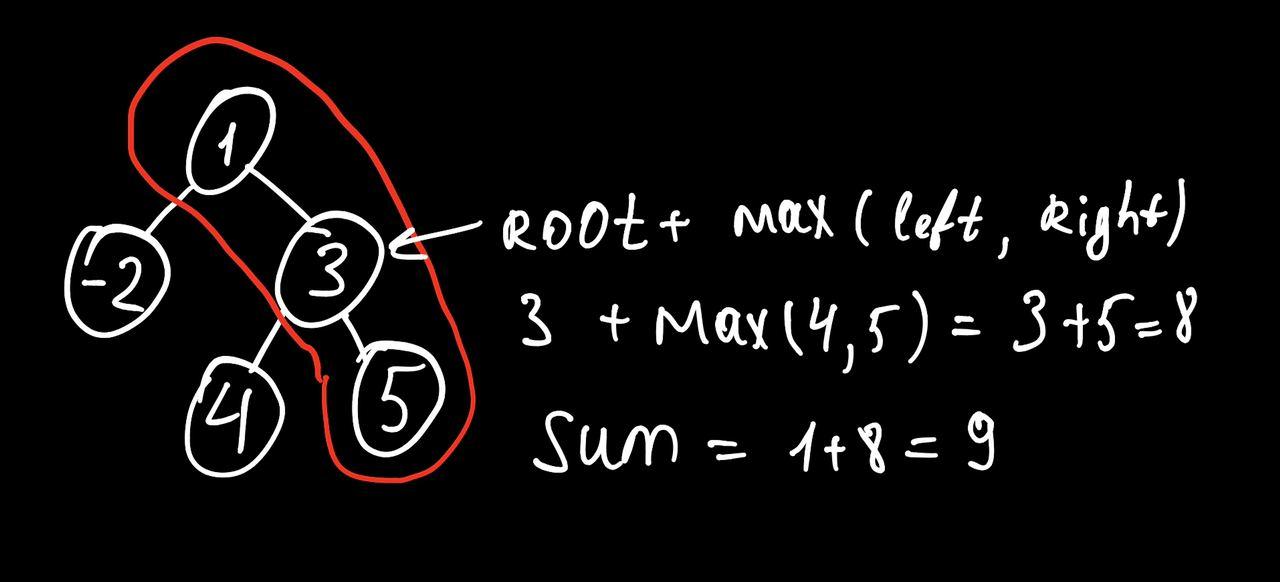
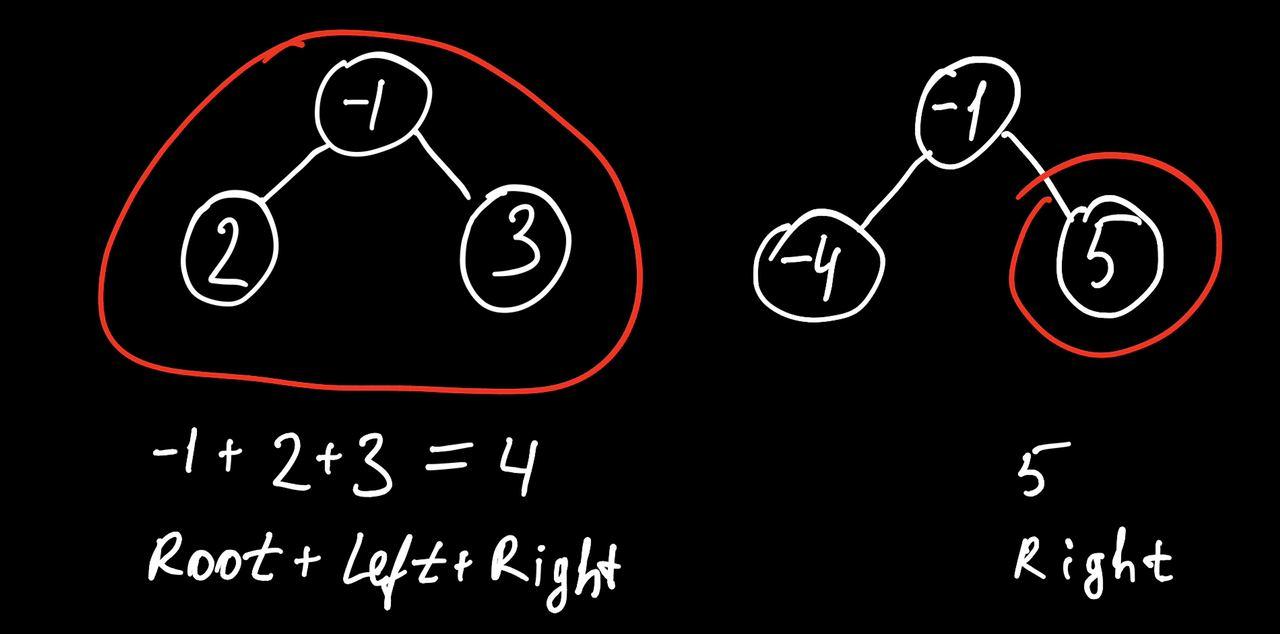
Algorithm

To find out the path we need to traverse the tree:

• we will use postorder traversal and
  • count the path sum
  • track the maximum value
• during the traversal we should take care of two cases:
  • Root + Left + Right
  • Root + Max(Left, Right)

Code

    public int MaxPathSum(TreeNode root)
    {
        if (root == null)
        {
            return 0;
        }

        int[] result = { int.MinValue };

        MaxPathSum(root, result);
        return result[0];
    }

    private static int MaxPathSum(TreeNode root, int[] result)
    {
        if (root == null)
        {
            return 0;
        }

        int left = Math.Max(0, MaxPathSum(root.Left, result));
        int right = Math.Max(0, MaxPathSum(root.Right, result));

        // track the maximum value
        result[0] = Math.Max(result[0], left + right + root.Value);
        return Math.Max(left, right) + root.Value;
    }

Time Complexity: O(n)